1. Introduction to 3D Rigid Transformations

1.1. Basics

Following Waldron and Schmiedeler [1], we define the basic terms that we use throughout this user guide.

	Position of a rigid body in 3D Euclidean space is expressed as a 3D vector.		Translation is a displacement, in which points move along parallel lines by the same distance.
	Orientation of a rigid body in 3D Euclidean space is defined by a set of 3 orthogonal basis vectors.		Rotation is a displacement, in which points move about a rotation axis through the origin of the reference frame (fixed point) along a circle by the same angle.
	Pose is a combination of position and orientation.		A (proper) rigid transformation is a combination of translation and rotation.

1.2. Frames

A (coordinate reference) frame in 3D Euclidean space is defined by an origin (position) and 3 orthogonal basis vectors (orientation) and it is attached to a rigid body. The pose (position and orientation) of a rigid body (i.e., of its frame) is always expressed with respect to another frame.

1.3. Frame Notation

Notation is important for describing and understanding of physical quantities in 3D. Furgale [2] [3] presents one of the most consistent and clear approaches and we use it here.

For physical quantities we use the notation \(_{A}\boldsymbol{x}_{BC}\), where \(\boldsymbol{x}\) is a physical quantity of frame C with respect to frame B expressed in frame A. For example, \(_{A}\boldsymbol{t}_{BC}\) is the translation of C with respect to B measured in A or \(_{A}\boldsymbol{\omega}_{BC}\) is the orientation vector of C with respect to B measured in A.

Since \(_A\boldsymbol{t}_{BC}\) represents a vector or translation from frame B to frame C expressed in frame A, the position of a point \(P\) with respect to a frame A in three-dimensional space can be defined by \(_A\boldsymbol{p} := _A\boldsymbol{t}_{AP}\).

When we define a mapping from some frame A to another frame B that can be expressed as a matrix multiplication, we use the notation \(\boldsymbol{M}_{BA}\) for the corresponding matrix. We can read this from right to left as a matrix that maps from frame A to frame B through multiplication, for example, when we want to transform a point by

\[_B\boldsymbol{p} = \boldsymbol{M}_{BA} {_A\boldsymbol{p}}\]

1.4. Duality of Transformations and Poses

We can use a transformation matrix \(\boldsymbol{T}_{BA}\) that represents a transformation from frame A to frame B to represent the pose (position and orientation) of frame A in frame B (if we use the active transformation convention; see Transformation Ambiguities and Conventions for details). This is just a different interpretation of the same matrix and similar to our interpretation of a vector from A to P \(_A\boldsymbol{t}_{AP}\) as a point \(_A\boldsymbol{p}\).

1.5. Representations

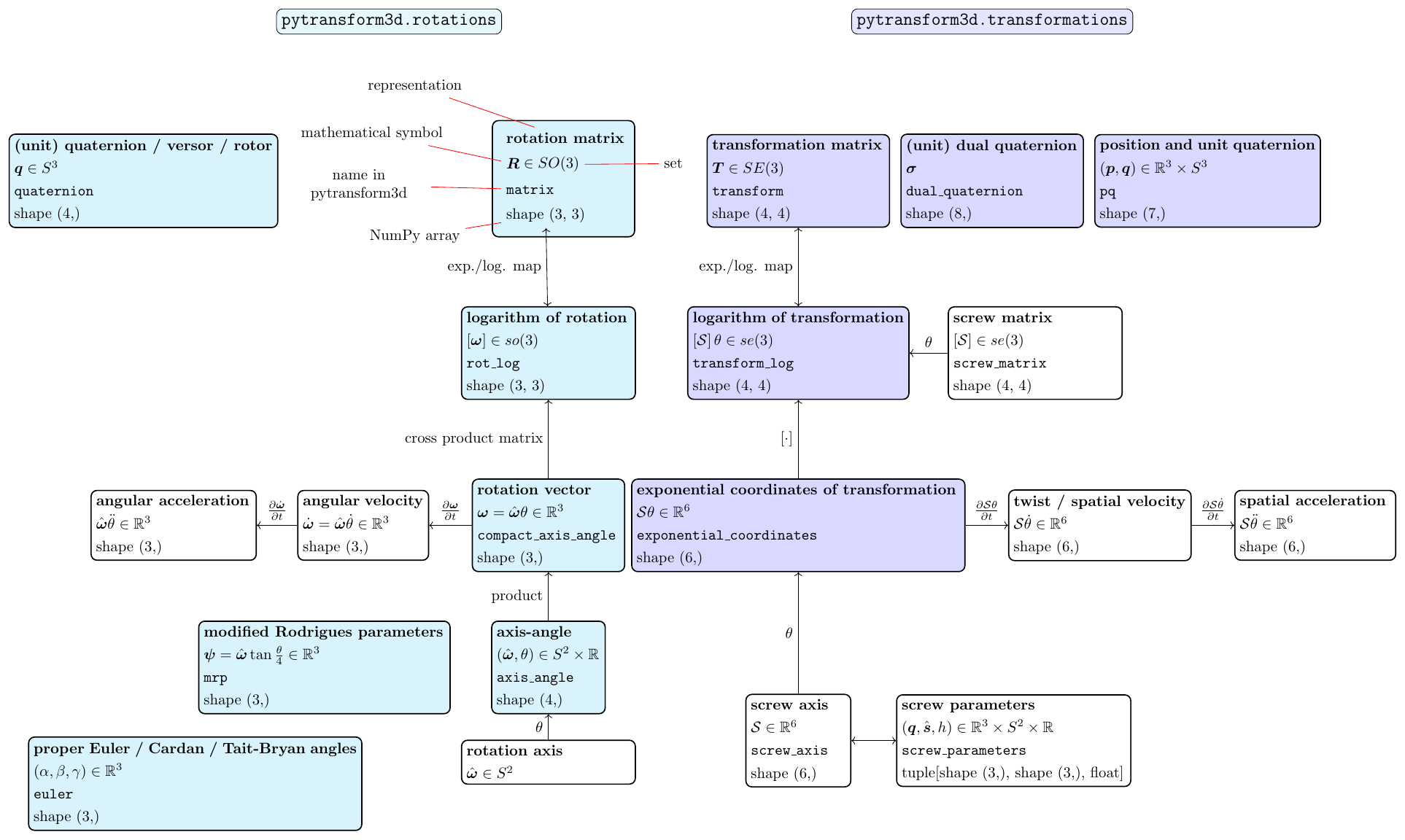
At least six numbers are required to express the pose of a rigid body or a transformation between two frames, but there are also redundant representations. We can use many different representations of rotation and / or translation. Here is an overview of the representations that are available in pytransform3d. All representations are stored in NumPy arrays, of which the corresponding shape is shown in this table. You will find more details on these representations on the following pages.

Representation and Mathematical Symbol	NumPy Array Shape	Rigid Transformation - SE(3)
		Rotation - SO(3)	Translation
Rotation matrix \(\pmb{R}\)	(3, 3)	X
Axis-angle \((\hat{\pmb{\omega}}, \theta)\)	(4,)	X
Rotation vector \(\pmb{\omega}\)	(3,)	X
Logarithm of rotation \(\left[\pmb{\omega}\right]\)	(3, 3)	X
Quaternion \(\pmb{q}\)	(4,)	X
Rotor \(R\)	(4,)	X
Euler angles \((\alpha, \beta, \gamma)\)	(3,)	X
Modified Rodrigues parameters \(\pmb{\psi}\)	(3,)	X
Transformation matrix \(\pmb{T}\)	(4, 4)	X	X
Exponential coordinates \(\mathcal{S}\theta\)	(6,)	X	X
Logarithm of transformation \(\left[\mathcal{S}\right]\theta\)	(4, 4)	X	X
Position and quaternion \((\pmb{p}, \pmb{q})\)	(7,)	X	X
Dual quaternion \(\boldsymbol{\sigma}\)	(8,)	X	X

1.6. References

[1]

Waldron, K., Schmiedeler, J. (2008). Kinematics. In: Siciliano, B., Khatib, O. (eds) Springer Handbook of Robotics. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-540-30301-5_2

[2]

Furgale, P. (2014). Representing Robot Pose: The good, the bad, and the ugly (slides). In What Sucks in Robotics and How to Fix It: Lessons Learned from Building Complex Systems (ICRA workshop). Note: these slides seem to be lost, but the blog below conveys the same message. http://static.squarespace.com/static/523c5c56e4b0abc2df5e163e/t/53957839e4b05045ad65021d/1402304569659/Workshop+-+Rotations_v102.key.pdf

[3]

Furgale, P. (2014). Representing Robot Pose: The good, the bad, and the ugly (blog). https://web.archive.org/web/20220420162355/http://paulfurgale.info/news/2014/6/9/representing-robot-pose-the-good-the-bad-and-the-ugly