4. Transformation Ambiguities and Conventions

Heterogeneous software systems that consist of proprietary and open source software are often combined when we work with transformations. For example, suppose you want to transfer a trajectory demonstrated by a human to a robot. The human trajectory could be measured from an RGB-D camera, fused with IMU sensors that are attached to the human, and then translated to joint angles by inverse kinematics. That involves at least three different software systems that might all use different conventions for transformations. Sometimes even one software uses more than one convention. The following aspects are of crucial importance to glue and debug transformations in systems with heterogenous and often incompatible software:

• Compatibility: Compatibility between heterogenous softwares is a difficult topic. It might involve, for example, communicating between proprietary and open source software or different languages.

• Conventions: Lots of different conventions are used for transformations in three dimensions. These have to be determined or specified.

• Conversions: We need conversions between these conventions to communicate transformations between different systems.

• Visualization: Finally, transformations should be visually verified and that should be as easy as possible.

pytransform3d assists in solving these issues. This documentation clearly states all of the used conventions, it aims at making conversions between rotation and transformation conventions as easy as possible, it is tightly coupled with Matplotlib to quickly visualize (or animate) transformations and it is written in Python with few dependencies. Python is a widely adopted language. It is used in many domains and supports a wide spectrum of communication to other software.

There are lots of ambiguities in the world of transformations. We try to explain them all here.

4.1. Right-handed vs. Left-handed Coordinate System

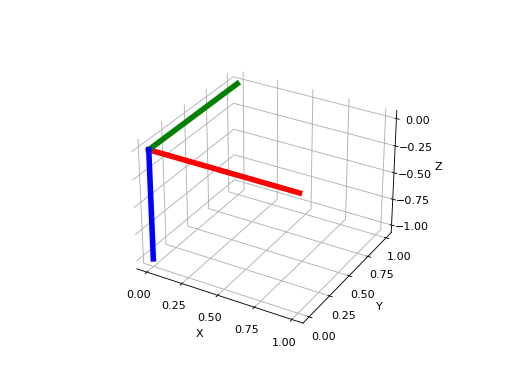
We typically use a right-handed coordinate system, that is, the x-, y- and z-axis are aligned in a specific way. The name comes from the way how the fingers are attached to the human hand. Try to align your thumb with the imaginary x-axis, your index finger with the y-axis, and your middle finger with the z-axis. It is possible to do this with a right hand in a right-handed system and with the left hand in a left-handed system.

Right-handed	Left-handed

Note

The default in pytransform3d is a right-handed coordinate system.

4.2. Active (Alibi) vs. Passive (Alias) Transformation

There are two different views of transformations: the active and the passive view [1] [2].

An active transformation

• changes the physical position of an object

• can be defined in the absence of a coordinate system or does not change the current coordinate system

• is the only convention used by mathematicians

Another name for active transformation is alibi transformation.

A passive transformation

• changes the coordinate system in which the object is described

• does not change the object

• could be used by physicists and engineers (e.g., roboticists)

Another name for passive transformation is alias transformation.

The following illustration compares the active view with the passive view. The position of the data is interpreted in the frame indicated by solid axes. We use exactly the same transformation matrix in both plots. In the active view, we see that the transformation is applied to the data. The data is physically moved. The dashed basis represents a frame that is moved from the base frame with the same transformation. The data is now interpreted in the old frame. In a passive transformation, we move the frame with the transformation. The data stays at its original position but it is interpreted in the new frame.

Active	Passive

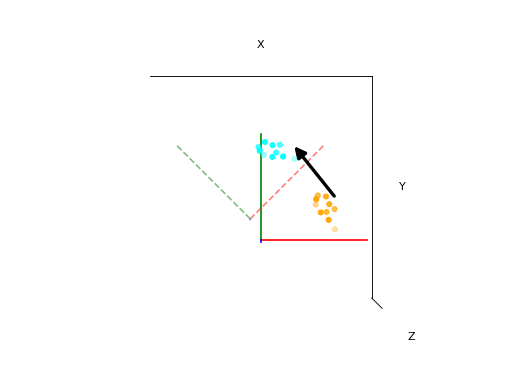
Using the inverse transformation in the active view gives us exactly the same solution as the original transformation in the passive view and vice versa.

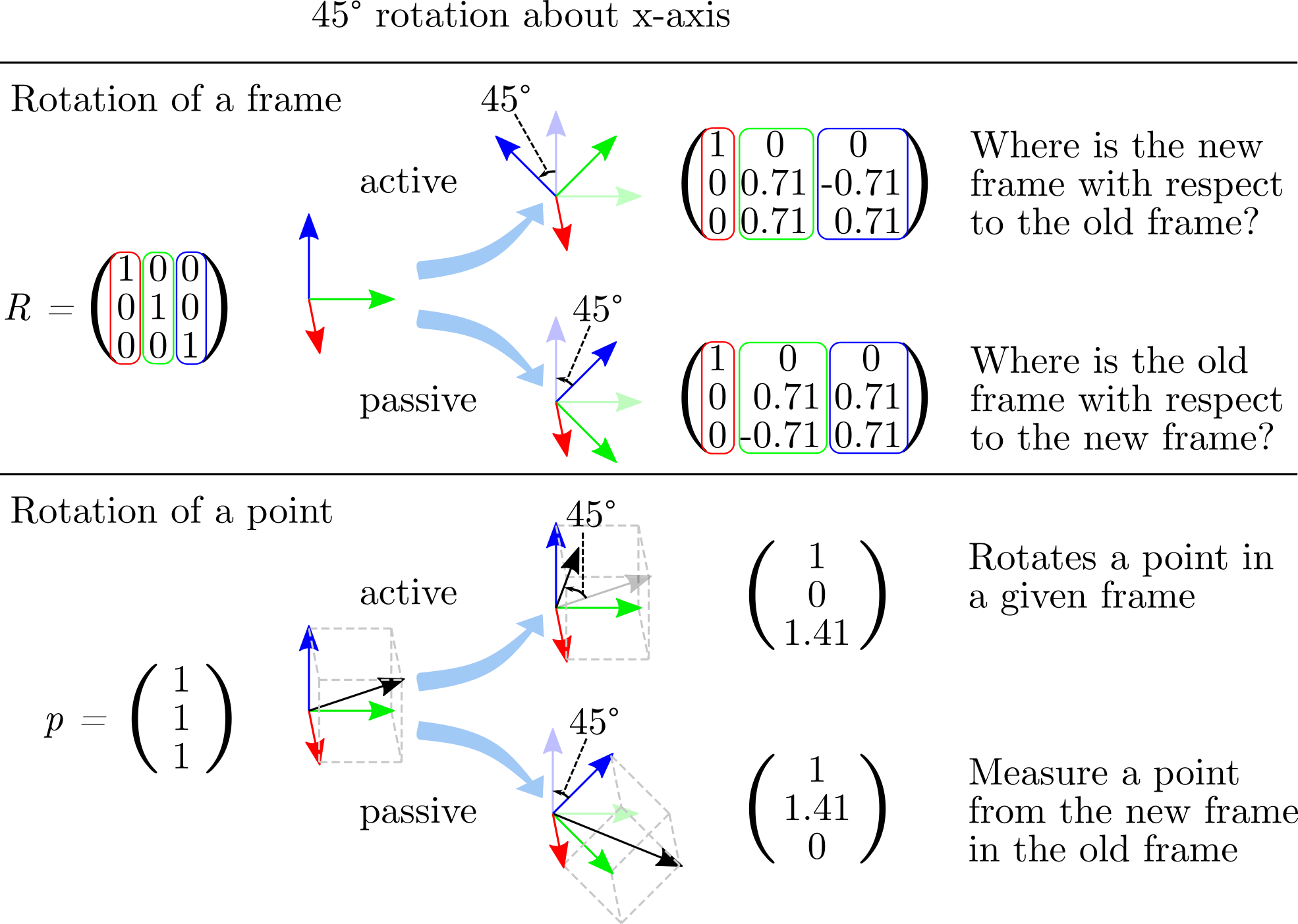
It is usually easy to determine whether the active or the passive convention is used by taking a look at the rotation matrix: when we rotate counter-clockwise by an angle \(\theta\) about the z-axis, the following rotation matrix is usually used in an active transformation:

\[\begin{split}\left( \begin{array}{ccc} \cos \theta & -\sin \theta & 0 \\ \sin \theta & \cos \theta & 0 \\ 0 & 0 & 1\\ \end{array} \right)\end{split}\]

Its transformed version is usually used for a passive transformation:

\[\begin{split}\left( \begin{array}{ccc} \cos \theta & \sin \theta & 0 \\ -\sin \theta & \cos \theta & 0 \\ 0 & 0 & 1\\ \end{array} \right)\end{split}\]

Warning

The standard in pytransform3d is an active rotation.

4.3. Pre-multiply vs. Post-multiply Rotations

The same point can be represented by a column vector \(\boldsymbol v\) or a row vector \(\boldsymbol w\). A rotation matrix \(\boldsymbol R\) can be used to rotate the point by pre-multiplying it to the column vector \(\boldsymbol R \boldsymbol v\) or by post-multiplying it to the row vector \(\boldsymbol w \boldsymbol R\). However, for the same rotation matrix, both approaches are inverse: \(\boldsymbol R^T \boldsymbol v = \boldsymbol w \boldsymbol R\). Hence, to achieve the same effect we have to use two different rotation matrices depending on how we multiply them to points.

Note

The default in pytransform3d are pre-multiplied rotation matrices.

4.4. Intrinsic vs. Extrinsic Transformations

A similar problem occurs when we want to concatenate rotations or transformations: suppose we have a rotation matrix \(R_1\) and another matrix \(R_2\) and we want to first rotate by \(R_1\) and then by \(R_2\). If we want to apply both rotations in global coordinates (global, space-fixed / extrinsic rotation), we have to concatenate them with \(R_2 \cdot R_1\). We can also express the second rotation in terms of a local, body-fixed coordinates (local, body-fixed / intrinsic rotation) by \(R_1 \cdot R_2\), which means \(R_1\) defines new coordinates in which \(R_2\) is applied. Note that this applies to both passive and active rotation matrices. Specifying this convention is particularly relevant when we deal with Euler angles.

Here is a comparison between various conventions of concatenation.

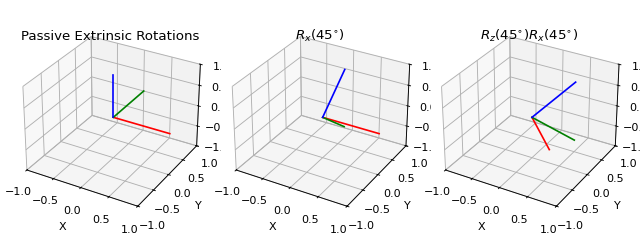
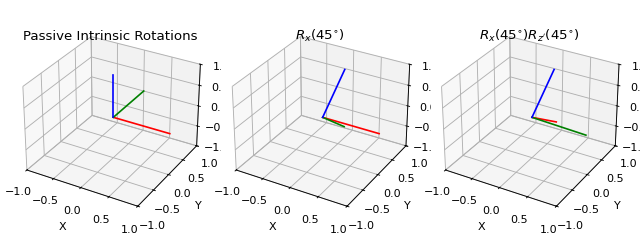
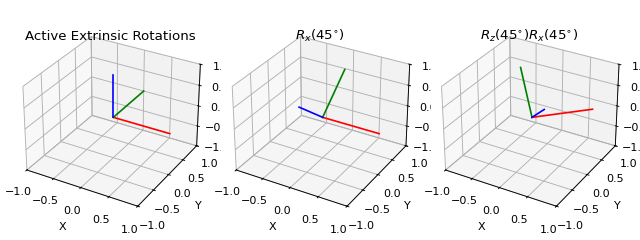
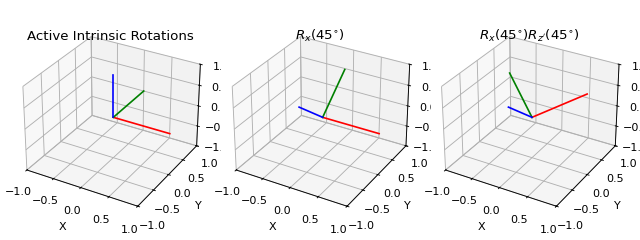
Warning

There are two conventions on how to concatenate rotations and transformations: intrinsic and extrinsic transformation. There is no default in pytransform3d but usually the function name should tell you which convention the function uses.

4.5. Naming and Frame Conventions

In addition to transformation and rotation conventions, there are a lot of different naming and frame conventions. Here are some examples.

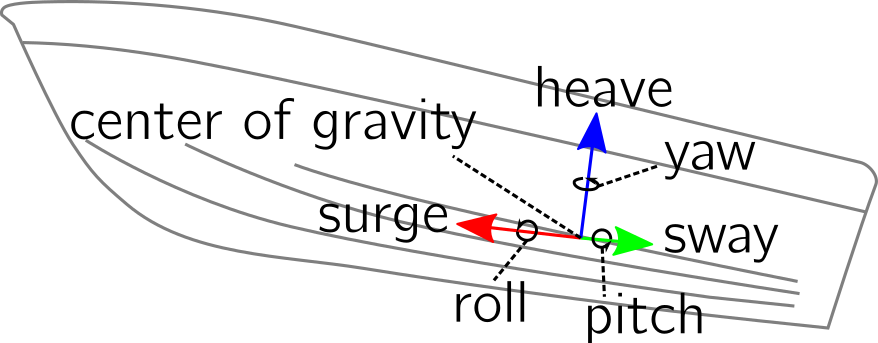
For ships we can use the following convention for the body frame: the x-axis is called surge, the y-axis sway, and the z-axis heave. The origin of the frame is the center of gravity. For the orientation, the names yaw, pitch, and roll are used. Sometimes the body frame is rotated by 180 degrees around the x-axis, so that the y-axis points to the right side and the z-axis down.

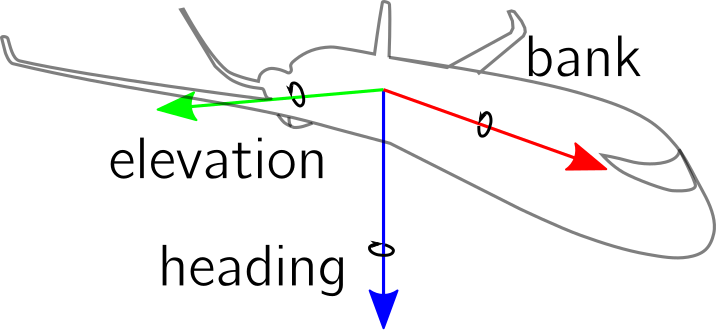
Aircrafts sometimes use the following naming conventions for intrinsic rotations around the z-, y’-, and x’’-axis. The rotation about the z-axis is called heading, rotation about the y’-axis is called elevation, and the rotation about the x’’-axis is called bank.

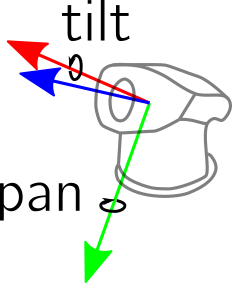
Cameras or similar sensors are sometimes mounted on pan/tilt units. Typically, first the pan joint rotates the camera about an axis parallel to the y-axis of the camera and the tilt joint rotates the camera about an axis parallel to the x-axis of the camera. When the axes of rotation and of the camera are not perfectly aligned, the camera will also be translated by the rotations.

4.6. Conventions of Other Software

The following is an incomplete list of conventions for representations of rotations, orientations, transformations, or poses and coordinate frames other software packages use. It illustrates the diversity that you will find when you combine different software systems.

Blender user interface (computer graphics)

• Active rotations

• Euler angles (are actually Tait-Bryan angles): external rotations, angles in degree

• Quaternion: scalar first

XSens MVNX format (motion capture)

• Active rotations

• Conventions for coordinate frames

  • Axis orientation in the world (global): x north, y west, z up (NWU)

  • Axis orientation on body parts: axes are aligned with world axes when subject stands in T pose

  • Quaternion and rotation matrix rotate from sensor frame to world frame, that is, they represent the orientation of the sensor with respect to the world

• Quaternion: scalar first

• Euler angles: extrinsic roll-pitch-yaw (xyz) convention

Bullet (physics engine)

• Active rotations

• Euler angles: extrinsic roll-pitch-yaw (xyz) convention (getQuaternionFromEuler from pybullet’s API)

• Quaternion: scalar last and Hamilton multiplication

Eigen (linear algebra library)

• Quaternion

  • Scalar first (constructor) and scalar last (internal)

  • Hamilton multiplication

Peter Corke’s robotics toolbox

• Active rotations

• Euler angles

  • Intrinsic zyz convention

  • Roll-pitch-yaw angles correspond either to intrinsic zyx convention (default) or intrinsic xyz convention, which can be selected by a parameter

• Quaternion: scalar first and Hamilton multiplication

Robot Operating System (ROS) (REP103)

• Active transformations

• Conventions for coordinate frames

  • Axis orientation on body: x forward, y left, z up

  • Axis orientation in the world: x east, y north, z up (ENU)

  • Axis orientation of optical camera frame (indicated by suffix in topic name): z forward, x right, y down

• Euler angles

  • Active, extrinsic roll-pitch-yaw (xyz) convention (as used, e.g., in origin tag of URDF) can be used

  • In addition, the yaw-pitch-roll (zyx) convention can be used, but is discouraged

• A PoseStamped is represented with respect to a frame_id

• When interpreted as active transformation, TransformStamped represents a transformation from child frame to its (parent) frame

• Quaternion: scalar last

Universal Robot user interface

• Conventions for coordinate frames

  • Default axis orientation of tool center point: z forward (approach direction), x and y axes define the orientation with which we approach the target

• Euler angles: extrinsic roll-pitch-yaw (xyz) convention

4.7. References

[1]

Selig, J.M. (2006): Active Versus Passive Transformations in Robotics. IEEE Robotics and Automation Magazine, 13(1), pp. 79-84, doi: 10.1109/MRA.2006.1598057. https://ieeexplore.ieee.org/document/1598057

[2]

Wikipedia: Active and passive transformation. https://en.wikipedia.org/wiki/Active_and_passive_transformation