5. Euler Angles

Since Euler angles [1] are an intuitive way to specify a rotation in 3D, they are often exposed at user interfaces. However, there are 24 different conventions that could be used. Furthermore, you have to find out whether degrees or radians are used to express the angles (we will only use radians in pytransform3d).

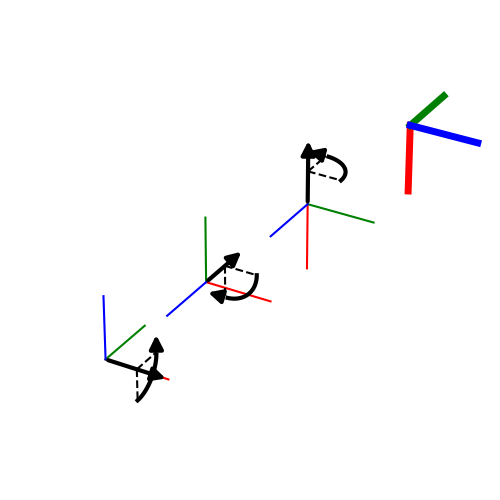
Here we rotate about the extrinsic (fixed) x-axis, y-axis, and z-axis by 90 degrees.

5.1. 24 Conventions

Euler angles generally refer to three consecutive rotations about basis vectors. There are proper Euler angles for which we can distinguish 6 conventions: xzx, xyx, yxy, yzy, zyz, and zxz. As you can see, proper Euler angles rotate about the same basis vector during the first and last rotation and they rotate about another basis vector in the second rotation. In addition, there are Cardan (or Tait-Bryan) angles that rotate about three different basis vectors. There are also 6 conventions: xzy, xyz, yxz, yzx, zyx, and zxy.

If you read about Transformation Ambiguities and Conventions, you know that the order in which we concatenate rotation matrices matters. We can make extrinsic rotations, in which we rotate about basis vectors of a fixed frame, and we can make intrinsic rotations, in which we rotate about basis vectors of the new, rotated frame. This increases the amount of possible conventions to \(2 (6 + 6) = 24\) (if we only allow active rotation matrices).

5.2. Range of Angles

Euler angles rotate about three basis vectors by the angles \(\alpha\), \(\beta\), and \(\gamma\). If we want to find the Euler angles that correspond to one rotation matrix \(\boldsymbol{R}\), there is an infinite number of solutions because we can always add or subtract \(2\pi\) to one of the angles and get the same result. In addition, for proper Euler angles

\[\boldsymbol{R}(\alpha, \beta, \gamma) = \boldsymbol{R}(\alpha + \pi, -\beta, \gamma - \pi).\]

For Cardan angles

\[\boldsymbol{R}(\alpha, \beta, \gamma) = \boldsymbol{R}(\alpha + \pi, \pi - \beta, \gamma - \pi).\]

For this reason the proper Euler angles are typically restricted to

\[-\pi \leq \alpha < \pi, \qquad 0 \leq \beta \leq \pi, \qquad -\pi \leq \gamma < \pi\]

and Cardan angles are usually restricted to

\[-\pi \leq \alpha < \pi, \qquad -\frac{\pi}{2} \leq \beta \leq \frac{\pi}{2}, \qquad -\pi \leq \gamma < \pi\]

to make these representations unique (using norm_euler()).

An alternative convention limits the range of \(\alpha\) and \(\gamma\) to \(\left[0, 2 \pi\right)\).

5.3. Gimbal Lock

The special case of a so-called gimbal lock occurs when the second angle \(\beta\) is at one of its limits. In this case the axis of rotation for the first and last rotation are either the same or exactly opposite, that is, an infinite number of angles \(\alpha\) and \(\gamma\) will represent the same rotation even though we restricted their range to an interval of length \(2\pi\): either all pairs of angles that satisfy \(\alpha + \gamma = constant\) or all pairs of angles that satisfy \(\alpha - \gamma = constant\). When we reconstruct Euler angles from a rotation matrix, we set one of these angles to 0 to determine the other. We can check if Euler angles are close to gimbal lock with euler_near_gimbal_lock().

5.4. Other Names

There are also other names for Euler angles. For example, the extrinsic xyz Cardan angles can also be called roll, pitch, and yaw (or sometimes the intrinsic convention is used here as well). Roll is a rotation about x, pitch is a rotation about y and yaw is a rotation about z.

5.5. References

[1]

Shuster, M. D. (1993). A Survery of Attitude Representations. The Journal of Astronautical Sciences, 41(4), pp. 475-476. http://malcolmdshuster.com/Pub_1993h_J_Repsurv_scan.pdf