10. Camera

When we know the 3D position of a point in the world we can easily compute where we would see it in a camera image with the pinhole camera model. However, we have to know some parameters of the camera:

• camera pose

• focal length \(f\)

• sensor width and height

• image width and height

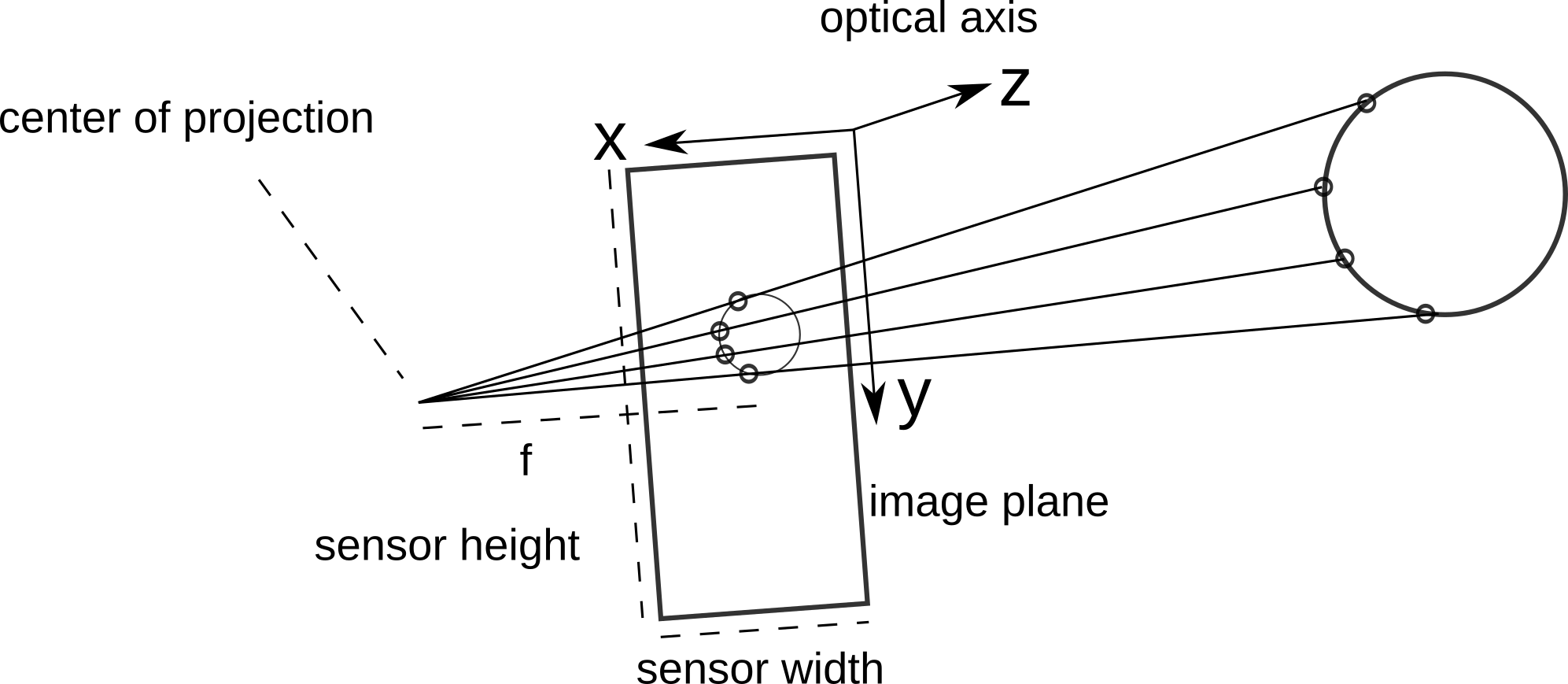
Note that light passes through a pinhole in a real pinhole camera before it will be measured from the sensor so that pixels will be mirrored in the x-y plane. The sensor that we show here actually corresponds to the virtual image plane.

The Example Camera Transform shows how a grid is projected on an image with the function world2image().

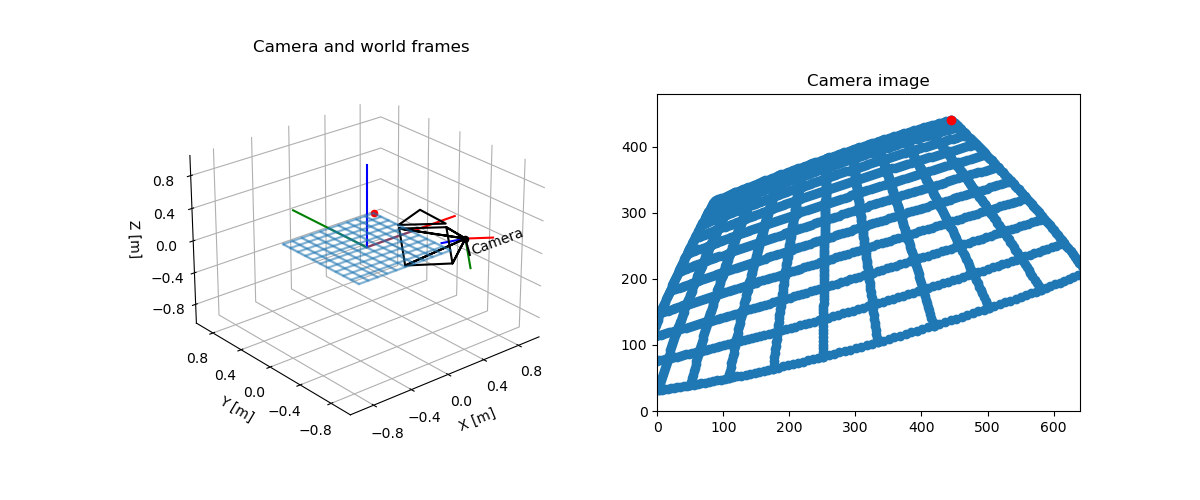
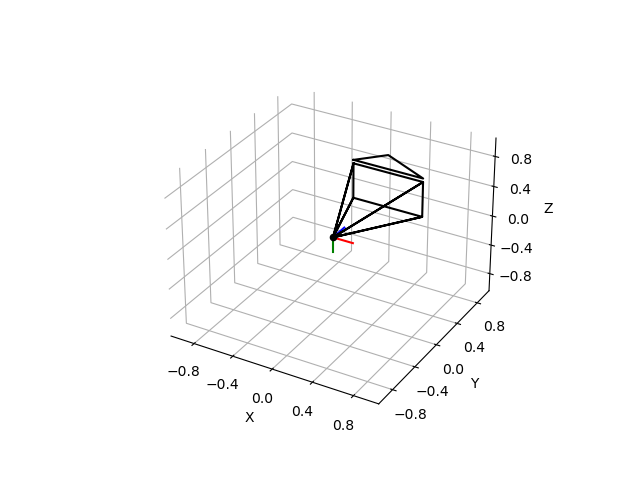
Extrinsic and intrinsic camera parameters can be visualized in the following way. The extrinsic camera parameters are fully determined by a transform from world coordinates to camera coordinates or by the pose of the camera in the world. In this illustration, the point indicates the camera center / center of projection, which is the position component of the pose. The orientation determines the direction to and orientation of the virtual image plane. The arrow at the top of the virtual image plane shows the up direction of the image.

The field of view is determined from the intrinsic camera parameters. These are given by a matrix

\[\begin{split}\left( \begin{array}{ccc} f_x & 0 & c_x\\ 0 & f_y & c_y\\ 0 & 0 & 1 \end{array} \right),\end{split}\]

where \(f_x, f_y\) are focal lengths and \(c_x, c_y\) is the position of the camera center. Together with the image size we can determine the field of view. Values of the intrinsic camera matrix and the image size can be given in pixels or meters to generate the following visualization with plot_camera() (see Example Camera Representation in 3D).

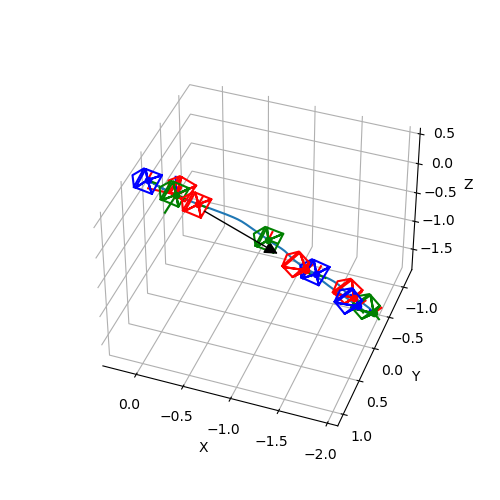
You can use this to display a trajectory of camera poses (see Example Camera Trajectory).