Dual Quaternion Interpolation

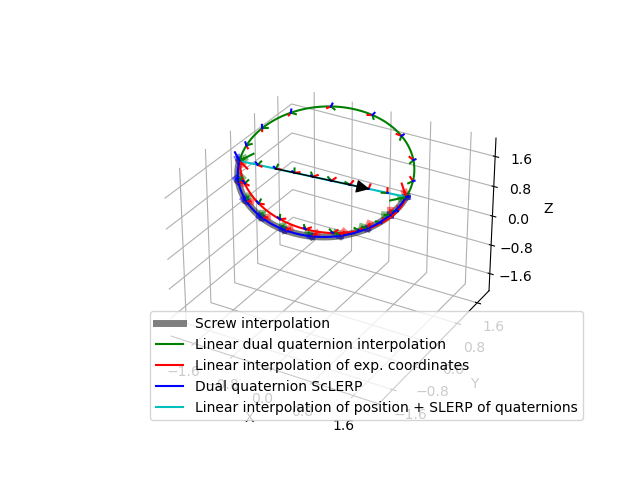
This example shows interpolated trajectories between two random poses. The red line corresponds to linear interpolation with exponential coordinates, the green line corresponds to linear interpolation with dual quaternions, and the blue line corresponds to screw linear interpolation (ScLERP) with dual quaternions. The true screw motion from pose 1 to pose 2 is shown by a thick, transparent black line in the background of the ScLERP interpolation.

import matplotlib.pyplot as plt
import numpy as np

import pytransform3d.plot_utils as ppu
import pytransform3d.trajectories as ptr
import pytransform3d.transformations as pt

Setup

We generate two random transformation matrices to represent two poses between we want to interpolate. These will also be converted to dual quaternions, exponential coordinates, and position and quaternion.

rng = np.random.default_rng(25)
pose1 = pt.random_transform(rng)
pose2 = pt.random_transform(rng)
dq1 = pt.dual_quaternion_from_transform(pose1)
dq2 = -pt.dual_quaternion_from_transform(pose2)
Stheta1 = pt.exponential_coordinates_from_transform(pose1)
Stheta2 = pt.exponential_coordinates_from_transform(pose2)
pq1 = pt.pq_from_transform(pose1)
pq2 = pt.pq_from_transform(pose2)

n_steps = 100

Ground Truth: Screw Motion

The ground truth for interpolation of poses is a linear interpolation of rotation about and translation along the screw axis. We will represent the difference between the two poses as exponential coordinates, a product of the screw axis and the magnitude of the transformation. We can use fractions of the exponential coordinates to smoothly interpolate between the two poses.

pose12pose2 = pt.concat(pose2, pt.invert_transform(pose1))
Stheta = pt.exponential_coordinates_from_transform(pose12pose2)
offsets = ptr.transforms_from_exponential_coordinates(
    Stheta[np.newaxis] * np.linspace(0, 1, n_steps)[:, np.newaxis]
)
interpolated_poses = ptr.concat_many_to_one(offsets, pose1)

Approximation: Linear Interpolation of Dual Quaternions

An approximately correct solution is linear interpolation and subsequent normalization of dual quaternions. The problem with dual quaternions is that they have a double cover and the path of the interpolation might be different depending on which of the two representation of the pose is selected. In this case the path does not match the ground truth path, but when we switch from dq1 to pt.dual_quaternion_double(dq1)—its alternative representation—the interpolation path is very close to the ground truth.

interpolated_dqs = (
    np.linspace(1, 0, n_steps)[:, np.newaxis] * dq1
    + np.linspace(0, 1, n_steps)[:, np.newaxis] * dq2
)
# renormalization (not required here because it will be done with conversion)
interpolated_dqs /= np.linalg.norm(interpolated_dqs[:, :4], axis=1)[
    :, np.newaxis
]
interpolated_poses_from_dqs = ptr.transforms_from_dual_quaternions(
    interpolated_dqs
)

Exact Solution: Screw Linear Interpolation (ScLERP)

Dual quaternions also support screw linear interpolation (ScLERP) which is implemented with the dual quaternion power. The dual quaternion power internally uses the screw parameters of the pose difference to smoothly interpolate along the screw axis.

sclerp_interpolated_dqs = np.vstack(
    [pt.dual_quaternion_sclerp(dq1, dq2, t) for t in np.linspace(0, 1, n_steps)]
)
sclerp_interpolated_poses_from_dqs = ptr.transforms_from_dual_quaternions(
    sclerp_interpolated_dqs
)

Approximation: Linear Interpolation of Exponential Coordinates

A more crude approximation is the linear interpolation of exponential coordinates.

interpolated_ecs = (
    np.linspace(1, 0, n_steps)[:, np.newaxis] * Stheta1
    + np.linspace(0, 1, n_steps)[:, np.newaxis] * Stheta2
)
interpolates_poses_from_ecs = ptr.transforms_from_exponential_coordinates(
    interpolated_ecs
)

Linear Interpolation of Position + SLERP

A completly different solution can be obtained by decomposing the poses into positions and orientations and then using spherical linear interpolation (SLERP) of the orientation (in this case: quaternions).

interpolated_pqs = np.vstack(
    [pt.pq_slerp(pq1, pq2, t) for t in np.linspace(0, 1, n_steps)]
)
interpolated_poses_from_pqs = ptr.transforms_from_pqs(interpolated_pqs)

Plotting

We show all solutions in one 3D plot.

ax = pt.plot_transform(A2B=pose1, s=0.3, ax_s=2)
pt.plot_transform(A2B=pose2, s=0.3, ax=ax)
traj = ppu.Trajectory(
    interpolated_poses, s=0.1, c="k", lw=5, alpha=0.5, show_direction=True
)
traj.add_trajectory(ax)
traj_from_dqs = ppu.Trajectory(
    interpolated_poses_from_dqs, s=0.1, c="g", show_direction=False
)
traj_from_dqs.add_trajectory(ax)
traj_from_ecs = ppu.Trajectory(
    interpolates_poses_from_ecs, s=0.1, c="r", show_direction=False
)
traj_from_ecs.add_trajectory(ax)
traj_from_dqs_sclerp = ppu.Trajectory(
    sclerp_interpolated_poses_from_dqs, s=0.1, c="b", show_direction=False
)
traj_from_dqs_sclerp.add_trajectory(ax)
traj_from_pq_slerp = ppu.Trajectory(
    interpolated_poses_from_pqs, s=0.1, c="c", show_direction=False
)
traj_from_pq_slerp.add_trajectory(ax)
plt.legend(
    [
        traj.trajectory,
        traj_from_dqs.trajectory,
        traj_from_ecs.trajectory,
        traj_from_dqs_sclerp.trajectory,
        traj_from_pq_slerp.trajectory,
    ],
    [
        "Screw interpolation",
        "Linear dual quaternion interpolation",
        "Linear interpolation of exp. coordinates",
        "Dual quaternion ScLERP",
        "Linear interpolation of position + SLERP of quaternions",
    ],
    loc="best",
)
plt.show()