Intrinsic#

We will compare all possible combinations of passive and active rotations and extrinsic and intrinsic concatenation of rotations.

import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import proj3d  # noqa: F401

from pytransform3d.rotations import (
    passive_matrix_from_angle,
    active_matrix_from_angle,
    plot_basis,
)

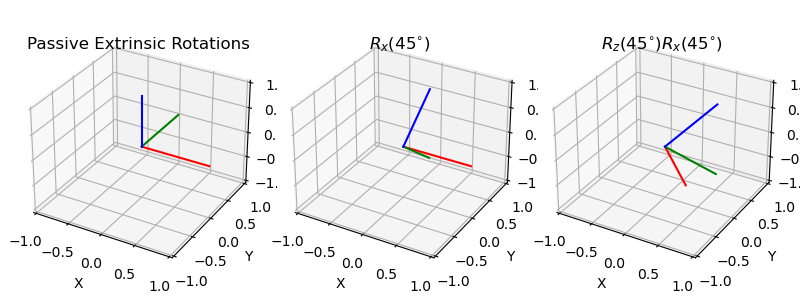
Passive Extrinsic Rotations#

plt.figure(figsize=(8, 3))
axes = [plt.subplot(1, 3, 1 + i, projection="3d") for i in range(3)]
for ax in axes:
    plt.setp(
        ax,
        xlim=(-1, 1),
        ylim=(-1, 1),
        zlim=(-1, 1),
        xlabel="X",
        ylabel="Y",
        zlabel="Z",
    )

Rx45 = passive_matrix_from_angle(0, np.deg2rad(45))
Rz45 = passive_matrix_from_angle(2, np.deg2rad(45))

axes[0].set_title("Passive Extrinsic Rotations", y=0.95)
plot_basis(ax=axes[0], R=np.eye(3))
axes[1].set_title("$R_x(45^{\circ})$", y=0.95)
plot_basis(ax=axes[1], R=Rx45)
axes[2].set_title("$R_z(45^{\circ}) R_x(45^{\circ})$", y=0.95)
plot_basis(ax=axes[2], R=Rz45.dot(Rx45))

plt.tight_layout()

$Passive Extrinsic Rotations, $R_x(45^{\circ})$, $R_z(45^{\circ}) R_x(45^{\circ})$$

/home/dfki.uni-bremen.de/afabisch/Projekte/pytransform3d/examples/plots/plot_convention_rotation_global_local.py:41: SyntaxWarning: invalid escape sequence '\c'
  axes[1].set_title("$R_x(45^{\circ})$", y=0.95)
/home/dfki.uni-bremen.de/afabisch/Projekte/pytransform3d/examples/plots/plot_convention_rotation_global_local.py:43: SyntaxWarning: invalid escape sequence '\c'
  axes[2].set_title("$R_z(45^{\circ}) R_x(45^{\circ})$", y=0.95)

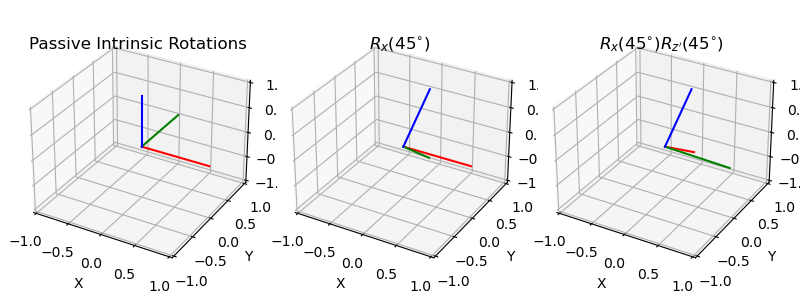
Passive Intrinsic Rotations#

plt.figure(figsize=(8, 3))
axes = [plt.subplot(1, 3, 1 + i, projection="3d") for i in range(3)]
for ax in axes:
    plt.setp(
        ax,
        xlim=(-1, 1),
        ylim=(-1, 1),
        zlim=(-1, 1),
        xlabel="X",
        ylabel="Y",
        zlabel="Z",
    )

axes[0].set_title("Passive Intrinsic Rotations", y=0.95)
plot_basis(ax=axes[0], R=np.eye(3))
axes[1].set_title("$R_x(45^{\circ})$", y=0.95)
plot_basis(ax=axes[1], R=Rx45)
axes[2].set_title("$R_x(45^{\circ}) R_{z'}(45^{\circ})$", y=0.95)
plot_basis(ax=axes[2], R=Rx45.dot(Rz45))

plt.tight_layout()

$Passive Intrinsic Rotations, $R_x(45^{\circ})$, $R_x(45^{\circ}) R_{z'}(45^{\circ})$$

/home/dfki.uni-bremen.de/afabisch/Projekte/pytransform3d/examples/plots/plot_convention_rotation_global_local.py:66: SyntaxWarning: invalid escape sequence '\c'
  axes[1].set_title("$R_x(45^{\circ})$", y=0.95)
/home/dfki.uni-bremen.de/afabisch/Projekte/pytransform3d/examples/plots/plot_convention_rotation_global_local.py:68: SyntaxWarning: invalid escape sequence '\c'
  axes[2].set_title("$R_x(45^{\circ}) R_{z'}(45^{\circ})$", y=0.95)

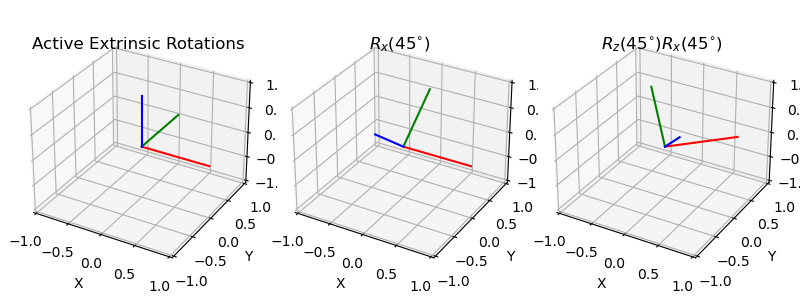
Active Extrinsic Rotations#

plt.figure(figsize=(8, 3))
axes = [plt.subplot(1, 3, 1 + i, projection="3d") for i in range(3)]
for ax in axes:
    plt.setp(
        ax,
        xlim=(-1, 1),
        ylim=(-1, 1),
        zlim=(-1, 1),
        xlabel="X",
        ylabel="Y",
        zlabel="Z",
    )

Rx45 = active_matrix_from_angle(0, np.deg2rad(45))
Rz45 = active_matrix_from_angle(2, np.deg2rad(45))

axes[0].set_title("Active Extrinsic Rotations", y=0.95)
plot_basis(ax=axes[0], R=np.eye(3))
axes[1].set_title("$R_x(45^{\circ})$", y=0.95)
plot_basis(ax=axes[1], R=Rx45)
axes[2].set_title("$R_z(45^{\circ}) R_x(45^{\circ})$", y=0.95)
plot_basis(ax=axes[2], R=Rz45.dot(Rx45))

plt.tight_layout()

$Active Extrinsic Rotations, $R_x(45^{\circ})$, $R_z(45^{\circ}) R_x(45^{\circ})$$

/home/dfki.uni-bremen.de/afabisch/Projekte/pytransform3d/examples/plots/plot_convention_rotation_global_local.py:94: SyntaxWarning: invalid escape sequence '\c'
  axes[1].set_title("$R_x(45^{\circ})$", y=0.95)
/home/dfki.uni-bremen.de/afabisch/Projekte/pytransform3d/examples/plots/plot_convention_rotation_global_local.py:96: SyntaxWarning: invalid escape sequence '\c'
  axes[2].set_title("$R_z(45^{\circ}) R_x(45^{\circ})$", y=0.95)

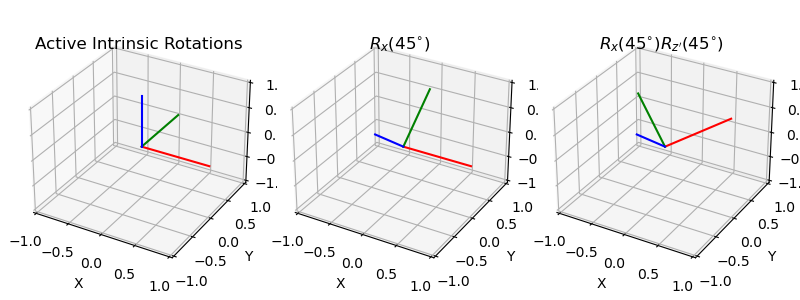
Active Intrinsic Rotations#

plt.figure(figsize=(8, 3))
axes = [plt.subplot(1, 3, 1 + i, projection="3d") for i in range(3)]
for ax in axes:
    plt.setp(
        ax,
        xlim=(-1, 1),
        ylim=(-1, 1),
        zlim=(-1, 1),
        xlabel="X",
        ylabel="Y",
        zlabel="Z",
    )

axes[0].set_title("Active Intrinsic Rotations", y=0.95)
plot_basis(ax=axes[0], R=np.eye(3))
axes[1].set_title("$R_x(45^{\circ})$", y=0.95)
plot_basis(ax=axes[1], R=Rx45)
axes[2].set_title("$R_x(45^{\circ}) R_{z'}(45^{\circ})$", y=0.95)
plot_basis(ax=axes[2], R=Rx45.dot(Rz45))

plt.tight_layout()

plt.show()

$Active Intrinsic Rotations, $R_x(45^{\circ})$, $R_x(45^{\circ}) R_{z'}(45^{\circ})$$

/home/dfki.uni-bremen.de/afabisch/Projekte/pytransform3d/examples/plots/plot_convention_rotation_global_local.py:119: SyntaxWarning: invalid escape sequence '\c'
  axes[1].set_title("$R_x(45^{\circ})$", y=0.95)
/home/dfki.uni-bremen.de/afabisch/Projekte/pytransform3d/examples/plots/plot_convention_rotation_global_local.py:121: SyntaxWarning: invalid escape sequence '\c'
  axes[2].set_title("$R_x(45^{\circ}) R_{z'}(45^{\circ})$", y=0.95)

Total running time of the script: (0 minutes 0.716 seconds)

Gallery generated by Sphinx-Gallery