Quaternion SLERP

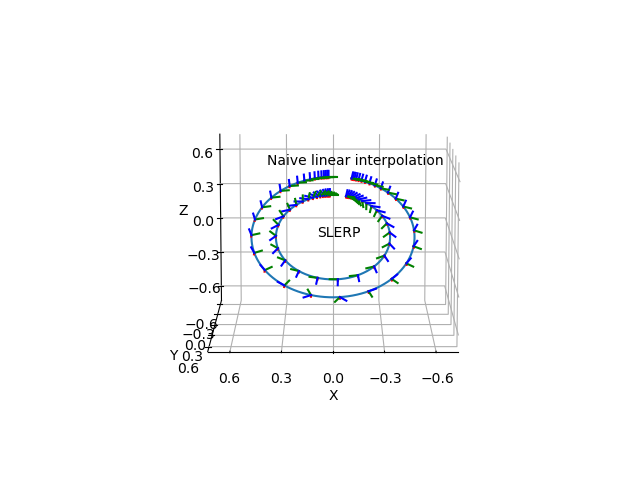
For small rotations, linear interpolation of quaternions gives almost the same results as spherical linear interpolation (SLERP). For larger angles there are significant differences as you can see in this example. The outer circle uses linear interpolation and the inner circle uses SLERP. You can play around with the value of ‘end_angle’ in this example.

import matplotlib.pyplot as plt
import numpy as np

from pytransform3d.rotations import (
    matrix_from_axis_angle,
    quaternion_from_matrix,
    quaternion_slerp,
)
from pytransform3d.trajectories import plot_trajectory

We assume the array T represents something like time. The position follows a sigmoid profile on a circular path over time, hence velocity is not constant.

T = np.linspace(0, 1, 1001)
sigmoid = 0.5 * (np.tanh(1.5 * np.pi * (T - 0.5)) + 1.0)
radius = 0.5
start_angle = np.deg2rad(0.0)
end_angle = np.deg2rad(350.0)

R1 = matrix_from_axis_angle([0, 0, 1, 0.5 * np.pi])
R2_start = matrix_from_axis_angle([1, 0, 0, start_angle])
R2_end = matrix_from_axis_angle([1, 0, 0, end_angle])
q_start = quaternion_from_matrix(R1.dot(R2_start))
q_end = quaternion_from_matrix(R1.dot(R2_end))

The naive linear interpolation method computes a time-weighted average between the orientation at the start and the orientation at the end.

lerp = np.zeros((len(T), 7))
lerp[:, 0] = radius * np.cos(np.deg2rad(90) - end_angle * sigmoid)
lerp[:, 2] = radius * np.sin(np.deg2rad(90) - end_angle * sigmoid)
if end_angle > np.pi:
    q_end *= -1.0
lerp[:, 3:] = (1.0 - T)[:, np.newaxis] * q_start + T[:, np.newaxis] * q_end

SLERP is the exact method to interpolate the orientations.

slerp = np.zeros((len(T), 7))
slerp[:, 0] = 0.7 * radius * np.cos(np.deg2rad(90) - end_angle * sigmoid)
slerp[:, 2] = 0.7 * radius * np.sin(np.deg2rad(90) - end_angle * sigmoid)
for i, t in enumerate(T):
    slerp[i, 3:] = quaternion_slerp(q_start, q_end, t)

The following 3D plot compares the two approaches.

ax = plot_trajectory(
    P=lerp, show_direction=False, n_frames=40, s=0.05, ax_s=0.7
)
ax = plot_trajectory(P=slerp, show_direction=False, n_frames=40, s=0.05, ax=ax)
ax.text(0.1, 0, 0, "SLERP")
ax.text(0.4, 0, 0.6, "Naive linear interpolation")
ax.view_init(elev=10, azim=90)
plt.show()