Concatenate Uncertain Transforms#

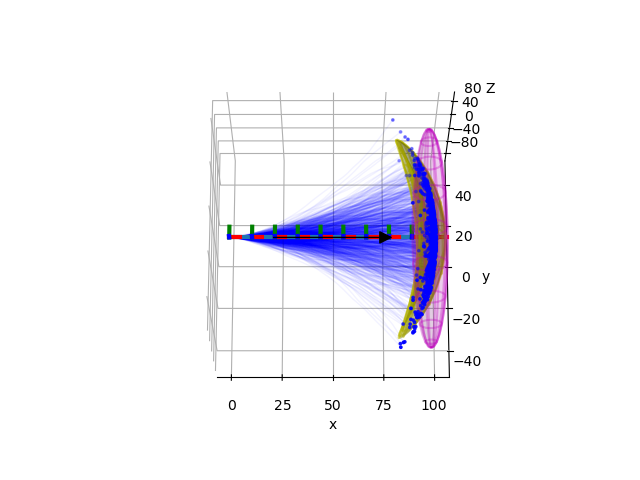
In this example, we assume that a robot is moving with constant velocity along the x-axis, however, there is noise in the orientation of the robot that accumulates and leads to different paths when sampling. Uncertainty accumulation leads to the so-called banana distribution, which does not seem Gaussian in Cartesian space, but it is Gaussian in exponential coordinates of SE(3).

This example adapted and modified to 3D from Barfoot and Furgale [1]. The banana distribution was analyzed in detail by Long et al. [2].

import numpy as np
import matplotlib.pyplot as plt
import pytransform3d.transformations as pt
import pytransform3d.trajectories as ptr
import pytransform3d.uncertainty as pu
import pytransform3d.plot_utils as ppu

We configure the example here. You can change the random seed if you want. We assume \(\Delta t = 1 s\) and constant velocity, so that in each step we concatenate the transformation \(\boldsymbol{T}_{vel}\) defined via its exponential coordinates here. The covariance associated with \(\boldsymbol{T}_{vel}\) is constructed from its Cholesky decomposition through \(\boldsymbol{LL}^T\). Since it is a diagonal matrix at the moment, we just define the standard deviation of each velocity component. In the default configuration we have some uncertainty in the rotational components of the velocity.

rng = np.random.default_rng(0)
cov_pose_chol = np.diag([0, 0.02, 0.03, 0, 0, 0])
cov_pose = np.dot(cov_pose_chol, cov_pose_chol.T)
velocity_vector = np.array([0, 0, 0, 1.0, 0, 0])
T_vel = pt.transform_from_exponential_coordinates(velocity_vector)
n_steps = 100
n_mc_samples = 1000
n_skip_trajectories = 1  # plot every n-th trajectory

We compute each path with respect to the initial pose of the robot, which we set to \(\boldsymbol{I}_{4 \times 4}\). The covariance of the initial pose is \(\boldsymbol{0}_{6 \times 6}\). We concatenate the current pose with \(\boldsymbol{T}_{vel}\) in each step and factor in the uncertainty of the pose and the transformation. Hence, uncertainties will accumulate in the covariance of the pose.

T_est = np.eye(4)
path = np.zeros((n_steps + 1, 6))
path[0] = pt.exponential_coordinates_from_transform(T_est)
cov_est = np.zeros((6, 6))
for t in range(n_steps):
    T_est, cov_est = pu.concat_globally_uncertain_transforms(
        T_est, cov_est, T_vel, cov_pose)
    path[t + 1] = pt.exponential_coordinates_from_transform(T_est)

We perform Monte-Carlo sampling of trajectories for comparison. This implementation is vectorized with NumPy.

T = np.eye(4)
mc_path = np.zeros((n_steps + 1, n_mc_samples, 4, 4))
mc_path[0, :] = T
for t in range(n_steps):
    noise_samples = ptr.transforms_from_exponential_coordinates(
        cov_pose_chol.dot(rng.standard_normal(size=(6, n_mc_samples))).T)
    step_samples = ptr.concat_many_to_one(noise_samples, T_vel)
    mc_path[t + 1] = np.einsum("nij,njk->nik", step_samples, mc_path[t])
# Plot the random samples' trajectory lines (in a frame attached to the start)
# same as mc_path[t, i, :3, :3].T.dot(mc_path[t, i, :3, 3]), but faster
mc_path_vec = np.einsum(
    "tinm,tin->tim", mc_path[:, :, :3, :3], mc_path[:, :, :3, 3])

We plot the MC-sampled trajectories and final poses, mean trajectory, projected equiprobably hyperellipsoid of the final distribution, and the equiprobably ellipsoid of the final distribution of the position.

ax = ppu.make_3d_axis(100)

for i in range(0, mc_path_vec.shape[1], n_skip_trajectories):
    ax.plot(
        mc_path_vec[:, i, 0], mc_path_vec[:, i, 1], mc_path_vec[:, i, 2],
        lw=1, c="b", alpha=0.05)
ax.scatter(
    mc_path_vec[-1, :, 0], mc_path_vec[-1, :, 1], mc_path_vec[-1, :, 2],
    s=3, c="b")

ptr.plot_trajectory(ax, ptr.pqs_from_transforms(
    ptr.transforms_from_exponential_coordinates(path)), s=5.0, lw=3)

pu.plot_projected_ellipsoid(
    ax, T_est, cov_est, wireframe=False, alpha=0.3, color="y", factor=3.0)
pu.plot_projected_ellipsoid(
    ax, T_est, cov_est, wireframe=True, alpha=0.5, color="y", factor=3.0)

mean_mc = np.mean(mc_path_vec[-1, :], axis=0)
cov_mc = np.cov(mc_path_vec[-1, :], rowvar=False)

ellipsoid2origin, radii = pu.to_ellipsoid(mean_mc, cov_mc)
ppu.plot_ellipsoid(
    ax, 3.0 * radii, ellipsoid2origin, wireframe=False, alpha=0.1, color="m")
ppu.plot_ellipsoid(
    ax, 3.0 * radii, ellipsoid2origin, wireframe=True, alpha=0.3, color="m")

plt.xlim((-5, 105))
plt.ylim((-50, 50))
plt.xlabel("x")
plt.ylabel("y")
ax.view_init(elev=70, azim=-90)
plt.show()

References#

Total running time of the script: (0 minutes 0.894 seconds)

Gallery generated by Sphinx-Gallery