pytransform3d.rotations.active_matrix_from_angle#
- pytransform3d.rotations.active_matrix_from_angle(basis, angle)[source]#
Compute active rotation matrix from rotation about basis vector.
With the angle \(\alpha\) and \(s = \sin{\alpha}, c=\cos{\alpha}\), we construct rotation matrices about the basis vectors as follows:
\[\begin{split}\boldsymbol{R}_x(\alpha) = \left( \begin{array}{ccc} 1 & 0 & 0\\ 0 & c & -s\\ 0 & s & c \end{array} \right)\end{split}\]\[\begin{split}\boldsymbol{R}_y(\alpha) = \left( \begin{array}{ccc} c & 0 & s\\ 0 & 1 & 0\\ -s & 0 & c \end{array} \right)\end{split}\]\[\begin{split}\boldsymbol{R}_z(\alpha) = \left( \begin{array}{ccc} c & -s & 0\\ s & c & 0\\ 0 & 0 & 1 \end{array} \right)\end{split}\]- Parameters:
- basisint from [0, 1, 2]
The rotation axis (0: x, 1: y, 2: z)
- anglefloat
Rotation angle
- Returns:
- Rarray, shape (3, 3)
Rotation matrix
- Raises:
- ValueError
If basis is invalid
Examples using pytransform3d.rotations.active_matrix_from_angle#
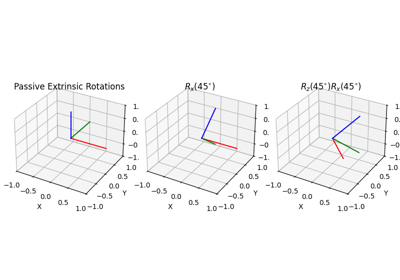
Convention for Rotation: Passive / Active, Extrinsic / Intrinsic
Convention for Rotation: Passive / Active, Extrinsic / Intrinsic