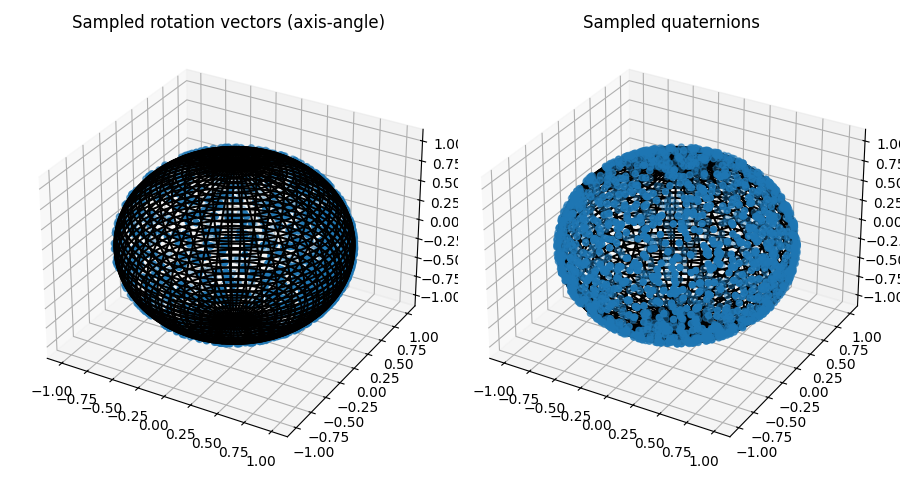
Compare Rotation Sampling Methods

There are different ways of sampling rotations. We draw random samples of rotations, convert them to rotation matrices, and apply these to the basis vector (1, 0, 0) to obtain points on the unit sphere.

import matplotlib.pyplot as plt
import numpy as np

import pytransform3d.batch_rotations as pbr
import pytransform3d.plot_utils as ppu
import pytransform3d.rotations as pr

rng = np.random.default_rng(1223532)
n_samples = 2000
v = np.array([1.0, 0.0, 0.0])

plt.figure(figsize=(9, 5))

ax1 = plt.subplot(121, projection="3d")
ax1.set_title("Sampled rotation vectors (axis-angle)")
ppu.plot_sphere(ax1, radius=1, n_steps=100)
rotations = np.vstack(
    [pr.random_compact_axis_angle(rng) for _ in range(n_samples)]
)
R = pbr.matrices_from_compact_axis_angles(rotations)
v_R = np.einsum("nij,j->ni", R, v)
ax1.scatter(v_R[:, 0], v_R[:, 1], v_R[:, 2])

ax2 = plt.subplot(122, projection="3d")
ax2.set_title("Sampled quaternions")
ppu.plot_sphere(ax2, radius=1, n_steps=100)
rotations = np.vstack([pr.random_quaternion(rng) for _ in range(n_samples)])
R = pbr.matrices_from_quaternions(rotations)
v_R = np.einsum("nij,j->ni", R, v)
ax2.scatter(v_R[:, 0], v_R[:, 1], v_R[:, 2])

plt.tight_layout()
plt.show()