Camera Projection

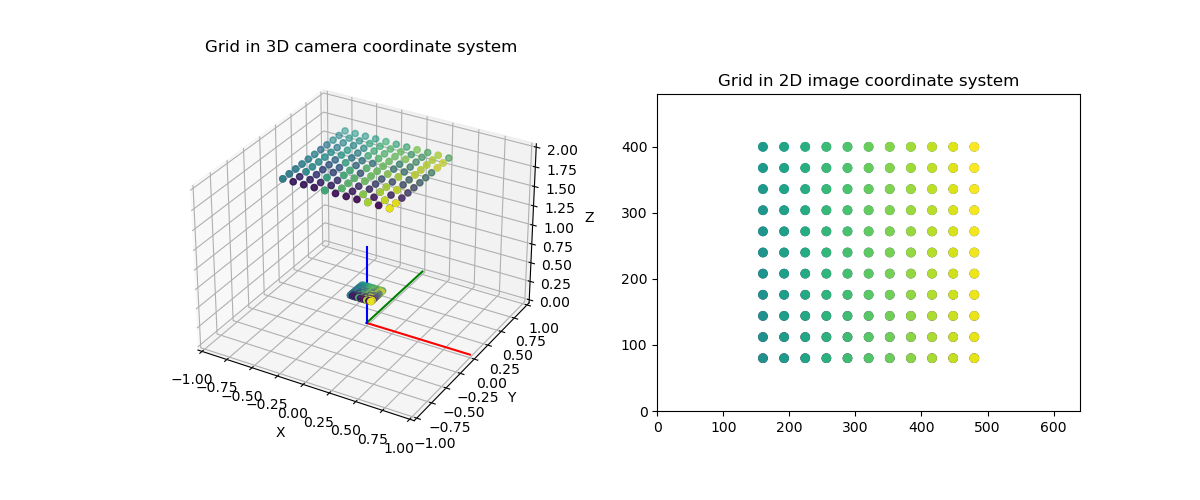
We can see the camera coordinate frame and a grid of points in the camera coordinate system which will be projected to the sensor. From the coordinates on the sensor we can compute the corresponding pixels.

import numpy as np
import matplotlib.pyplot as plt
from pytransform3d.transformations import plot_transform
from pytransform3d.camera import make_world_grid, cam2sensor, sensor2img

Camera Details

We have to define the focal length and sensor size of the camera in meters as well as the image size in pixels. The sensor size is extraordinarily large so that we can see it.

focal_length = 0.2
sensor_size = (0.2, 0.15)
image_size = (640, 480)

Grid

We define a grid in 3D world coordinates and compute its projection to the sensor in 3D.

cam_grid = make_world_grid(n_points_per_line=11) - np.array([0, 0, -2, 0])
img_grid_3d = cam_grid * focal_length

Projection

First, we project the grid from its original 3D coordinates to its projection on the sensor, then we convert it to image coordinates.

sensor_grid = cam2sensor(cam_grid, focal_length)
img_grid = sensor2img(sensor_grid, sensor_size, image_size)

Plotting

Now we can plot the grid in 3D, projected to the 3D sensor, and projected to the image.

plt.figure(figsize=(12, 5))
ax = plt.subplot(121, projection="3d")
ax.set_title("Grid in 3D camera coordinate system")
ax.set_xlim((-1, 1))
ax.set_ylim((-1, 1))
ax.set_zlim((0, 2))
ax.set_xlabel("X")
ax.set_ylabel("Y")
ax.set_zlabel("Z")
c = np.arange(len(cam_grid))
ax.scatter(cam_grid[:, 0], cam_grid[:, 1], cam_grid[:, 2], c=c)
ax.scatter(img_grid_3d[:, 0], img_grid_3d[:, 1], img_grid_3d[:, 2], c=c)
plot_transform(ax)

ax = plt.subplot(122, aspect="equal")
ax.set_title("Grid in 2D image coordinate system")
ax.scatter(img_grid[:, 0], img_grid[:, 1], c=c)
ax.set_xlim((0, image_size[0]))
ax.set_ylim((0, image_size[1]))

plt.show()