pytransform3d.rotations.matrix_from_axis_angle#
- pytransform3d.rotations.matrix_from_axis_angle(a)[source]#
Compute rotation matrix from axis-angle.
This is called exponential map or Rodrigues’ formula.
\[\boldsymbol{R}(\hat{\boldsymbol{\omega}}, \theta) = Exp(\hat{\boldsymbol{\omega}} \theta) = \cos{\theta} \boldsymbol{I} + \sin{\theta} \left[\hat{\boldsymbol{\omega}}\right] + (1 - \cos{\theta}) \hat{\boldsymbol{\omega}}\hat{\boldsymbol{\omega}}^T = \boldsymbol{I} + \sin{\theta} \left[\hat{\boldsymbol{\omega}}\right] + (1 - \cos{\theta}) \left[\hat{\boldsymbol{\omega}}\right]^2\]This typically results in an active rotation matrix.
- Parameters:
- aarray-like, shape (4,)
Axis of rotation and rotation angle: (x, y, z, angle)
- Returns:
- Rarray, shape (3, 3)
Rotation matrix
Examples using pytransform3d.rotations.matrix_from_axis_angle#
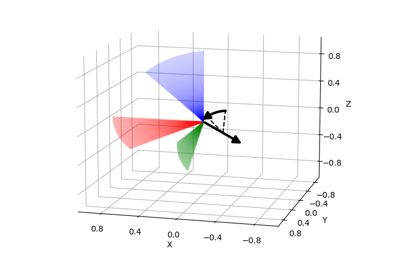
Axis-Angle Representation from Two Direction Vectors
Axis-Angle Representation from Two Direction Vectors